ECUACIÓN LINEAL HOMOGÉNEA
CONCEPTO:
Es aquella ecuación que se representa mediante el decremento de la derivada igualando la ecuación a cero. Por lo contrario se trata de una ecuación lineal no homogénea si se iguala a un número diferente de cero.
E. L. H. an(x) dny/dx`` + an(x) dn-1y/dxn-1 + .... a2(x) d2y/dx2 + a1(x) dy/dx + a0(x)y = 0
E.L.N.H. an(x) dny/dx`` + an(x) dn-1y/dxn-1 + .... a2(x) d2y/dx2 + a1(x) dy/dx + a0(x)y = g(x)
FUENTE:
- M. en E. Luis Gustavo García Flores
ALGORITMO:
1. Se tiene una ecuación diferencial homogénea
2. Dicha ecuación se convierte a una ecuación polinomial encontando las raíces de ésta.
3. Cuando la solución tiene raíces reales éstas deben ser linealmente independientes
4. Se sustituyen los valores en la fórmula y= c1 e^m1x + c2 e^m2x
5. Se obtiene el resultado
6. Fin
EJEMPLO:










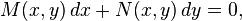
 y
y  son iguales. Esto es equivalente a decir que existe una función
son iguales. Esto es equivalente a decir que existe una función 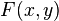 tal que:
tal que:
 y
y  .
. .
.





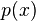
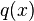

![y(x) =e^{ - \int_{x_0}^x p(s) ds } \left[ y_0 + \int_{x_0}^x q(s) e^{ \int_{x_0}^s \! p(t) dt } ds \right]](https://upload.wikimedia.org/math/e/a/7/ea72db1c1a628bea4e95070c0ac796d5.png)
