ECUACIONES DIFERENCIALES LINEALES
CONCEPTO:
Las Ecuaciones diferenciales de primer orden se caracterizan por ser de la forma:
Donde 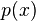 y
y 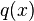 son funciones continuas en un intervalo abierto
son funciones continuas en un intervalo abierto  . La solución de esta ecuación viene dada por:
. La solución de esta ecuación viene dada por:
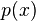 y
y 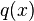 son funciones continuas en un intervalo abierto
son funciones continuas en un intervalo abierto  . La solución de esta ecuación viene dada por:
. La solución de esta ecuación viene dada por:
FUENTE:
- https://es.wikipedia.org/wiki/Ecuaci%C3%B3n_diferencial_lineal
ALGORITMO:
1. Identificar el factor integrante M=e^p(x)dx
2. Multiplicar la ecuación diferencial por el factor integrante
3. Sustituir en el primer miembro la derivada del producto de la función por el factor integral d/dx y* M
4. Integrar la ecuación y despejar la variable independiente
5. Obtener la solución integral
6. Fin
EJEMPLO:

![y(x) =e^{ - \int_{x_0}^x p(s) ds } \left[ y_0 + \int_{x_0}^x q(s) e^{ \int_{x_0}^s \! p(t) dt } ds \right]](https://upload.wikimedia.org/math/e/a/7/ea72db1c1a628bea4e95070c0ac796d5.png)

No hay comentarios:
Publicar un comentario