ECUACIONES DIFERENCIALES LINEALES
(solución particular)
CONCEPTO:
Una ecuación diferencial lineal ordinaria es una ecuación diferencial que tiene la forma:
Para que una ecuación diferencial sea lineal debe darse que no aparezcan productos de la función incógnita consigo misma ni con ninguna de sus derivadas. Si usamos la notación  para denotar el operador diferencial lineal de la ecuación anterior, entonces la ecuación anterior puede escribirse como:
para denotar el operador diferencial lineal de la ecuación anterior, entonces la ecuación anterior puede escribirse como:
 para denotar el operador diferencial lineal de la ecuación anterior, entonces la ecuación anterior puede escribirse como:
para denotar el operador diferencial lineal de la ecuación anterior, entonces la ecuación anterior puede escribirse como:
Las Ecuaciones diferenciales de primer orden se caracterizan por ser de la forma:
Donde 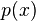 y
y 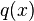 son funciones continuas en un intervalo abierto
son funciones continuas en un intervalo abierto  . La solución de esta ecuación viene dada por:
. La solución de esta ecuación viene dada por:
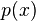 y
y 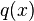 son funciones continuas en un intervalo abierto
son funciones continuas en un intervalo abierto  . La solución de esta ecuación viene dada por:
. La solución de esta ecuación viene dada por:![y(x) =e^{ - \int_{x_0}^x p(s) ds } \left[ y_0 + \int_{x_0}^x q(s) e^{ \int_{x_0}^s \! p(t) dt } ds \right]](https://upload.wikimedia.org/math/e/a/7/ea72db1c1a628bea4e95070c0ac796d5.png)
FUENTE:
- https://es.wikipedia.org/wiki/Ecuaci%C3%B3n_diferencial_lineal
ALGORITMO:
1. Identificar el factor integrante M= e^p(x)dx
2. Multiplicar la ecuación diferencial por el factor integrante
3. Sustituir en el primer miembro la derivada del producto de la función por el factor integral d/dx y*M
4. Integrar la ecuación y despejar la variable independiente
5. Obtener la solución general
6. Despejar "c"
7. Sustituir los valores de los puntos (x,y) en "c"
8. Y obtener el valor de "c"
9. Sustituir el valor de "c" en la solución general
10. Obtener la solución particular y hacer lo mismo para los otros puntos dados
11. Hacer una tabla dándole valores a "x" de -3 a 3
12. Sustituir esos valores en la solución particular y resolver
13. Obtener valores para "y"
14. Graficar
15. Fin
EJEMPLO:
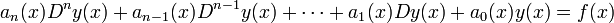




No hay comentarios:
Publicar un comentario