ECUACIÓN DIFERENCIAL EXACTA
(solución particular)
CONCEPTO:
En matemáticas, una ecuación diferencial exacta es una ecuación diferencial ordinaria de primer orden que presenta la forma:
donde las derivadas parciales de las funciones M y N:  y
y  son iguales. Esto es equivalente a decir que existe una función
son iguales. Esto es equivalente a decir que existe una función 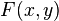 tal que:
tal que:
 y
y  son iguales. Esto es equivalente a decir que existe una función
son iguales. Esto es equivalente a decir que existe una función 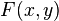 tal que:
tal que:
donde  y
y  .
.
 y
y  .
.
Dado que 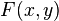 es una función diferenciable, entonces, por el teorema de Clairaut, sus derivadas cruzadas deben ser iguales. Esto significa que:
es una función diferenciable, entonces, por el teorema de Clairaut, sus derivadas cruzadas deben ser iguales. Esto significa que:
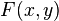 es una función diferenciable, entonces, por el teorema de Clairaut, sus derivadas cruzadas deben ser iguales. Esto significa que:
es una función diferenciable, entonces, por el teorema de Clairaut, sus derivadas cruzadas deben ser iguales. Esto significa que: .
.
FUENTE:
- https://es.wikipedia.org/wiki/Ecuaci%C3%B3n_diferencial_exacta
ALGORITMO:
1. Comprobar que sea una ecuación diferencial exacta
2. Integrar a la función M(x,y)dx con respecto a "x" y sustituir a la constante "c" por la función c=h(y)
3. Se deriva a la función encontrada con respecto a "y" y se iguala con la función N(x,y)
4. Se integra la función con respecto a la variable "y" y se despejan h(y)
5. Se encuentra la solución general con la ecuación de el paso 2, sustituyendo el valor de h(y) e igualando con una constante de integración.
6. Sustituir los puntos (x,y) en "c"
7. Obtener el valor de "c"
8. sustituir el valor de "c" en la solución general
9 Y se obtiene la sol particular
10. Hacer lo mismo para los otros puntos dados.
11. Graficar
12. Fin
12. Fin
EJEMPLO:
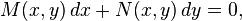






No hay comentarios:
Publicar un comentario